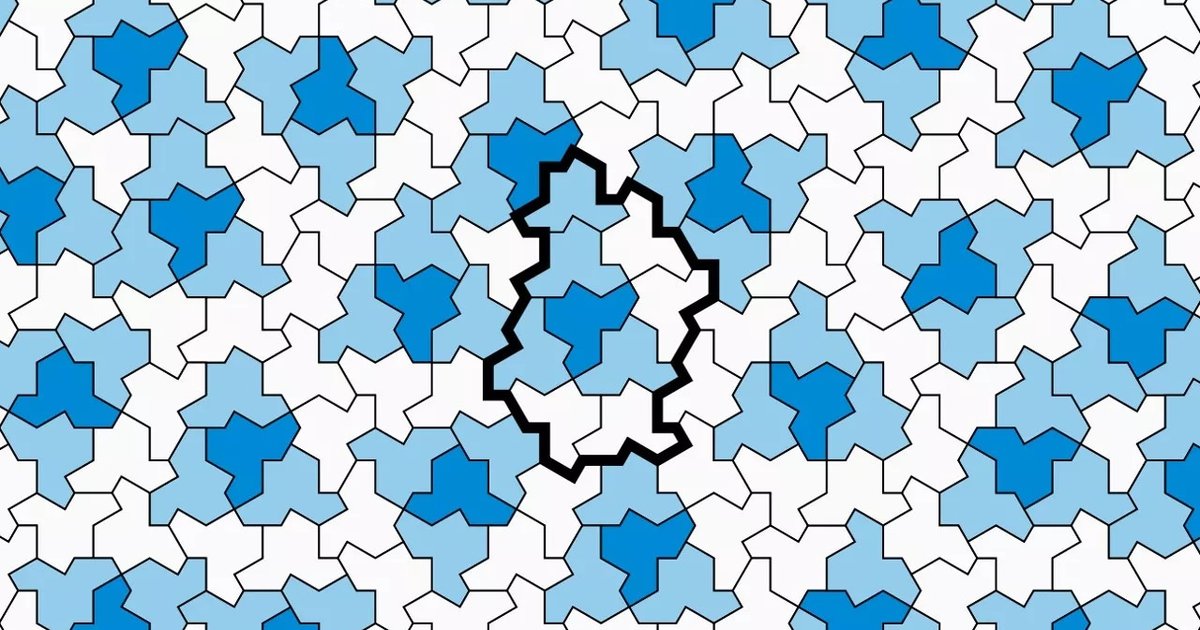
Похоже, найден идеальный рисунок плитки для ванной комнаты. Если выложить фигуру в виде мозаики, то она покроет всю плоскость. При этом узор никогда не повторится.

Команда исследователей во главе с математиком Дэвидом Смитом создала новую фигуру, существование которой было предсказано теоретически. Она получила странное название — «шляпа» (the hat), пишет Gizmodo.

Речь идет о так называемой «эйнштейновской» апериодической моноплитке. Эта такая форма, которой можно покрыть всю поверхность без какой-либо трансляционной симметрии и без повторения ее узора. 

В 1961 году математик Хао Ван предположил, что апериодическая мозаика не может существовать. Но его ученик Роберт Бергер все-таки подобрал набор из 20 426 фигур, которые при тщательном упорядочении никогда не повторялись. Затем он сократил список до 104 плиток. Это означает, что если бы вы купили набор этих плиток и разложили бы их на полу в ванной, то никогда не смогли бы найти повторяющийся рисунок.